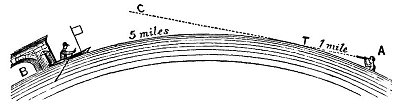
FIG. 2.
A boat, with a flag-staff, the top of the flag 5 feet above the surface of the water, was directed to sail from a place called "Welche's Dam" (a well-known ferry passage), to another called "Welney Bridge." These two points are six statute miles apart. The author, with a good telescope, went into the water; and with the eye about 8 inches above the surface, observed the receding boat during the whole period required to sail to Welney Bridge. The flag and the boat were distinctly visible throughout the whole distance! There could be no
mistake as to the distance passed over, as the man in charge of the boat had instructions to lift one of his oars to the top of the arch the moment he reached the bridge. The experiment commenced about three o'clock in the afternoon of a summer's day, and the sun was shining brightly and nearly behind or against the boat during the whole of its passage. Every necessary condition had been fulfilled, and the result was to the last degree definite and satisfactory. The conclusion was unavoidable that the surface of the water for a length of six miles did not to any appreciable extent decline or curvate downwards from the line of sight. But if the earth is a globe, the surface of the six miles length of water would have been 6 feet higher in the centre than at the two extremities, as shown in diagram fig. 2; but as the telescope was only 8 inches above the
water, the highest point of the surface would have been at one mile from the place of observation; and below this point the surface of the water at the end of the remaining five miles would have been 16 feet.
Let A B represent the arc of water 6 miles long, and A C the line of sight. The point of contact with the arc would be at T, a distance of one mile from the observer at A. From T to the bridge at B would be 5 miles, and the curvature from T to B would be 16 feet 8 inches. The top of the flag on the boat (which was 5 feet high) would have been 11 feet 8 inches below
the horizon T, and altogether out of sight. Such a condition was not observed; but the following diagram, fig. 3, exhibits the true state of the case--A, B, the line of sight, equi-distant.
from or parallel with the surface of the water throughout the whole distance of 6 milts: From which it is concluded that the surface of standing water is not convex, but horizontal.